AlexeySpace.Ru
Программирование трехмерной графики. Часть 3.
В предыдущих статьях мы познакомились с основами программирования трехмерной графики. Научились строить трехмерные точки и проецировать их на экран нашего монитора. А также научились производить с ними основные операции по перемещению в их пространстве.
Вершины (точки в пространстве) – это основа (каркас) всех трехмерных объектов. Из вершин собираются полигоны, а из полигонов – сложные трехмерные объекты.
Что же такое полигон? Взгляните на рисунок (3.1.1.).
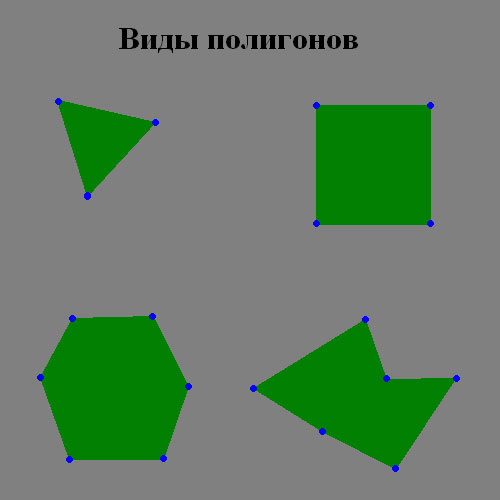
Т.е. по рисунку видно, что полигон – это геометрическая фигура, состоящая из отрезков, последовательно соединенных своими концами в замкнутую фигуру. Треугольник, квадрат, прямоугольник являются частными случаями полигона.
Полигон (polygon), в переводе с английского – это многоугольник. Просто у нас термин “многоугольник” – используются в основном в геометрии. А термин “полигон” прикрепился именно к понятиям трехмерной графики. А по сути - это одно и тоже.
Что бы определить наш треугольник создадим такую структуру:
Структура TVertex описывает точку в пространстве, а массив TTriangle – описывает наш полигон. Для построения треугольника, достаточно трех точек. Поэтому наш массив состоит из трех элементов, которые определяют координаты вершин треугольника.
Теперь давайте определим наш, треугольник. Для этого создадим переменную типа TTriangle, и зададим ей следующие координаты:
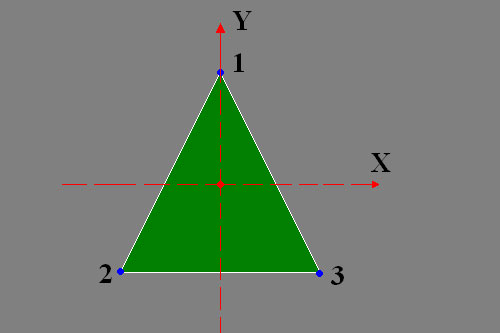
Координаты у нас задаются следующим образом: т.к. точка (0,0,0) – это центр экрана, то первая вершина у нас лежит на оси oY и имеет значение Y = 100; вторая вершина лежит в левой нижней части графика и имеет координаты: X = -100; Y = - 100; третья точка соответственно лежит напротив второй и имеет координаты: X = 100; Y = - 100.
Как видно, координату Z мы не учитываем (присваиваем ей ноль), т.е. наш треугольник будет параллелен координатной плоскости XY. См. рисунок (3.1.2.).
В Delphi у класса Canvas – есть замечательная функция рисования полигонов.
В качестве параметра мы передаем этой функции массив точек (TPoint), а функция соединяет все эти точки в полигон. Кол-во точек в массиве может быть не ограничено.
Если вы программирует в какой-нибудь другой среде, то можно воспользоваться WinAPI – функцией рисования полигона.
В качестве параметров, в эту функцию передается графический контекст устройства “DC”, на котором будет происходить вывод графики, массив точек “Points”, и количество этих точек “Count”.
Теперь рассмотрим функцию рисования нашего треугольника:
Тут все просто. Сначала мы очищаем экран. Потом совершаем поворот трех точек нашего треугольника вокруг координатной оси. (Формулы поворота были подробно разобраны во второй статье). Потом получившиеся точки переводим в двухмерные, и соответственно эти точки соединяем в полигон. Ниже Вы можете скачать пример рисования нашего треугольника.
Скачать исходник Delphi. [3 Кб]Скачать демонстрационную программу. [155 Кб]Простейший полигон рисовать мы уже научились. Теперь давайте нарисуем что-нибудь посложнее. Сейчас мы нарисуем не просто один полигон, а целую трехмерную фигуру. Это конечно же будет куб. Так как эта простая фигура, и на ней легко показать принципы построения трехмерных объектов.
Для построения квадрата нам потребуется четыре вершины, поэтому объявляем тип TQuad – следующим образом:
У куба шесть сторон, поэтому нам потребуется шесть квадратов, т.е. шесть переменных типа TQuad. Объявляем этот массив в программе:
Первый индекс в двухмерном массиве определяет номер квадрата, второй индекс – номер вершины данного квадрата.
Теперь для всех шести квадратов нам нужно задать их координаты в пространстве, так же как мы делали для треугольника.
Получился довольно таки большой кусок кода инициализации куба. Но тут ничего сложного нет. Мы задаем координаты вершин каждой стороне куба: верхней, нижней, задней и т.д…
И наконец, осталось немного переделать нашу процедуру рисования графики. Получится следующее:
Вместо одного треугольника, нам теперь нужно нарисовать шесть квадратов. Поэтому проходимся по массиву FQuads, и выполняем поворот для всех вершин входящих в каждый квадрат. Для наглядности мы поворачиваем вершины сначала по оси XY, а потом по XZ.
Потом переводим координаты каждого квадрата в двухмерное представление, и по очереди рисуем их с помощью функции Polygon. Т.е. в эту функцию уже пихается массив из четырех точек, а не из трех, когда мы рисовали треугольник.
Скачать исходник Delphi. [3 Кб]Скачать демонстрационную программу. [155 Кб]Теперь попробуем немного модифицировать нашу программу. Давайте в процедуре рисования графики, изменить цвет рамки наших квадратов с зеленого на белый.
Запустите программу, и вы увидите, что получилось не очень красиво. Дело в том, что наши полигоны рисуются в неправильной последовательности. Например, задний полигон вдруг выходит на передний план, хотя на самом деле он должен рисоваться самым первым. Т.е. самые отдаленные от экрана полигоны должны рисоваться самыми первыми, а более близкие к экрану, последними. При рисовании более близкие полигоны должны накладываться на уже нарисованные более отдаленные полигоны, тогда трехмерная сцена будет отображаться верно. Для этого и существует метод сортировки полигонов, от более отдаленного от экрана, до самого близкого. Или по другому его еще называют – удаление невидимых граней.
Геометрически это непростая задача. Во всех видеокартах, задача удаления невидимых граней уже давно решена на аппаратном уровне. Там используется Z-буффер. У нас же нет доступа к видеокарте, и мы рисуем стандартными функциями Window для вывода графики. Поэтому нам придется решать эту задачу геометрически.
К счастью, куб – очень простая фигура. Поэтому отсортировать его полигоны нам будет очень просто.
Для начала немного модифицируем наши типы данных:
Мы добавили новый тип - TVector. Это-то же самое, что и TVertex. Этот тип мы добавили просто для удобства программирования. Так же мы изменили тип TQuad. Теперь это не просто массив, а структура. Сюда вошли три новых поля. Color – цвет полигона. Point2D –двухмерная проекция нашей вершины. Теперь мы будем после перевода вершины в 2D, сразу заносить их в это поле. Normal – нормаль полигона.
На последнем остановимся поподробнее. Что такое нормаль, и зачем она нужна? Во-первых, нормаль – это перпендикуляр. Т.е. в нашем случае перпендикуляр к нашему полигону. Во-вторых – это вектор. И в-третьих, длинна этого вектора всегда равна единице.
В трехмерной графике нормали используются в основном для просчета освещения объектов. Т.е., чем больше угол между нормалью и вектором света, тем больше будет освещен наш полигон. А приводить эту нормаль к единичной длине нужно для упрощения математических вычислений во время прорисовки графики.
Допустим, у нас есть два вектора A1(x1, y1, z1) и B1(x2, y2, z2). Формула нахождения угла между ними выглядит следующим образом:
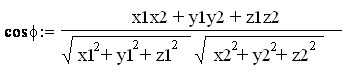
Т.е. скалярное произведения векторов нужно разделить на произведение длин этих векторов. Но так как длинны векторов у нас равны единице, то нижнюю часть формулы можно легко отбросить. Получится вот такая простая формула:
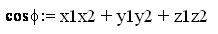
Поэтому нормали для всех полигонов вычисляются заранее, что бы потом во время отрисовки графики, тратить меньше компьютерных ресурсов для вычисления углов между нормалями.
При инициализации куба, каждая его сторона будет перпендикулярна одной из оси координат, поэтому можно задать следующие координаты нормалей:
С помощью этих нормалей мы и будем сортировать наши полигоны. А точнее по координате Z – каждой нормали. Т.е. полигоны с самым меньшим значением будут рисоваться самыми первыми, а полигоны с большими значениями этой координаты, рисуются последними.
Это самый простой способ сортировки полигонов, но и подходит он только для простых объектов. Куба, сферы и других выпуклых фигур. Для трехмерных моделей с уже более-менее сложной структурой этот способ уже работать не будет. В таких случаях нам придется использовать сложные алгоритмы удаления невидимых граней, например - алгоритм художника.
Сортировать наши полигоны мы будем с помощью метода быстрой сортировки. Когда у нас полигонов немного, в нашем случае их шесть – этот метод не дает ощутимой прибавки в производительности. Но вот когда число их зашкаливает за тысячу, выигрыш в быстродействии будет уже ощутимый. Поэтому будем использовать только эту сортировку.
Теперь рассмотрим процедуру рисования нашего куба:
Как видно процедура рисования куба у нас уже значительно усложнилась. Теперь мы выполняем поворот не только вершин куба, но и все его нормали. Т.е. нормаль полигон у нас должна вращаться в туже сторону, что и сам полигон.
Затем переводим все наши вершины в двухмерный вид. Т.е. заполняем массив Points2D – каждого полигона. Потом сортируем полигоны по координате Z. И наконец выводим их на экран.
Скачать исходник Delphi. [4 Кб]Скачать демонстрационную программу. [155 Кб]Так как расчет нормалей в нашей программе мы уже реализовали, то добавить освещение к нашему кубу уже не составит больших проблем. Для начала давайте превратим наш тип TQuad в полноценный класс.
Т.к. TQuad – теперь стал классом, то перед началом работы с ним, нам сначала нужно будет создать объекты этого класса, что бы с ними работать. Т.е. создать шесть полигонов. Делается это просто:
А в событии уничтожения формы нам нужно освободить эти объекты. Делается это тоже просто:
Теперь у нас поле Color – является не просто переменной класса, теперь она является свойством класса. При попытки присвоить этому полю какой-либо значение, т.е. присвоить ему цвет – будет вызываться процедура SetColor. А при попытки извлечь из этого поля значение цвета, будет соответственно вызываться функция GetColor.
Вот реализация этих методов:
Метод SetColor раскладывает наш цвет на RGB – составляющую. И присваивается приватной переменной класса FRGB. Приватная переменная (поле) – это переменная, которая будет доступна только внутри нашего класса (в методах нашего класса).
А вот в методе GetColor и происходит самой интересное. В этом методе мы RGB цвета конвертируем обратно в тип TColor. При этом предварительно умножая каждую составляющую цвета на его интенсивность. А интенсивность цвета у нас будет определяться переменной Normal.Z, т.е. Z – координатой нормали нашего полигона.
Почему так? Да очень просто! Договоримся, что источник света у нас будет направлен на экран монитора. Т.е. световые лучи будут направлены как бы из глаз человека сидящего перед монитором. Поэтому вектор светового луча будет параллелен координатной оси Z. Т.е. координаты вектора луча света будут следующие: (0, 0, 1);
Этот вектор тоже единичный. А как мы уже узнали, найти угол между двумя единичными векторами можно по формуле angle = X1X2 + Y1Y2 + Z1Z2.
Подставляем наши вектора в эту формулу и получаем: Normal.X * 0 + Normal.Y * 0 + Normal.Z * 1. Отсюда видно переменная Normal.Z и будет коэффициентом угла между нормалью полигона и вектором луча света. Все просто!
Чем больше значение Normal.Z будет приближаться к единице, тем меньше будет угол между нормалью и лучом света и тем соответственно больше будет интенсивность цвета.
Мы рассмотрели самый простейший вид освещения, и наверно это способ освещения единственный, который можно реализовать с помощью графических классов Delphi. Но я надеюсь, что этого было достаточно, что бы понять, по какому принципу в 3D графики рассчитываются источники света.
Скачать исходник Delphi. [4 Кб]Скачать демонстрационную программу. [155 Кб]
Комментарии (5):
Мне тоже все 3 статьи понравилось. Все логично, понятно и доступно.
Спасибо!
Добавить комментарий: